Se encontraron 108 resultados sin ingresar un término de búsqueda
- Curso de Francés B1.2 Gratis
En este curso de Francés B1.2 obtendrás las habilidades necesarias para llevar tus habilidades lingüísticas al siguiente nivel. Conocerás el vocabulario, gramática y pronunciación en este idioma para que puedas entablar desde conversaciones informales hasta discusiones más complejas, te prepararemos para comunicarte con éxito en cualquier contexto. Además, este curso de Francés B1.2 te prepará para interactuar con hablantes nativos con un grado razonable de fluidez y espontaneidad. Aprenderás a narrar experiencias, describir sueños, esperanzas y metas, así como a dar breves razones y explicaciones para tus opiniones y planes. ¿A quién está dirigido? Este curso de Francés B1.2 está diseñado para estudiantes del idioma francés que deseen mejorar sus habilidades lingüísticas, personas interesadas en la cultura francesa, estudiantes que preparan exámenes de nivel B1, viajeros que quieran mejorar su comunicación en francés, o cualquier persona que desee fortalecer sus competencias lingüísticas para fines personales o profesionales. Curso de Francés B1.2 [Gratis y Certificado]
- ¿Cómo se forja una katana japonesa?
¿Cómo se forja una katana japonesa? La Forja del Alma Japonesa en Acero. Adéntrate en un mundo donde el acero no solo es un material, sino una filosofía. Nuestro último post te invita a descubrir un pequeño documental que captura un proceso casi mítico: la forja de una clásica Katana Wakizashi japonesa en la actualidad. Este no es solo un vistazo a la metalurgia; es una inmersión profunda en una forma de vida milenaria que venera la paciencia, la precisión y la conexión espiritual con el material. ¿Qué verás? Desde la transformación del legendario "acero joya", pasando por el laborioso plegado que define el alma de la hoja, hasta el toque final del pulido que revela su Hamon (línea de temple). ¿Qué aprenderás? Más allá del filo, este documental es una ventana a la cultura japonesa: la reverencia por los ancestros, la disciplina inquebrantable y la profunda ética de trabajo de un maestro forjador. Es un viaje de fuego, martillo y tradición que te dejará con ganas de explorar mucho más sobre esta cultura. ¡No te lo pierdas!
- Bugonia | 2025 | Yorgos Lanthimos | Sub Esp y Esp Latino
Audio en Esp. Latino
- Brave Browser | Buscador recomendado para ver películas y series sin anuncios
Brave Browser Te recomendamos usar este buscador para evitar la publicidad y ventanas emergentes al reproducir series y películas. Te garantizamos que la experiencia al reproducir contenido cambiará completamente, ¡No te lo pierdas! Haz clic en la imagen para descargarlo.
- Curso de marketing digital | Gratis
Este curso de marketing digital es de acceso gratuito e incluye opción de Certificación Internacional. A lo largo del curso de marketing digital de Edutin Academy, adquirirás conocimientos en la gestión de redes sociales, creación de campañas publicitarias. Descubrirás cómo interpretar tendencias del mercado, aprovechar las plataformas digitales eficazmente y construir una narrativa persuasiva que resuene con tu audiencia. A lo largo de este curso de marketing digital, desarrollarás habilidades para crear campañas exitosas, medir el impacto de tus estrategias de marketing, comprender la investigación de mercado y análisis de la competencia, crear sitios web efectivos e implementar CTAs convincentes. Aprenderás sobre la publicidad SEM y SEO, cómo crear anuncios en redes sociales, email marketing y realizar análisis de datos para impulsar y optimizar tus estrategias. ¿A quién está dirigido?👨💼👩💻💡 Este curso de marketing digital está diseñado para emprendedores que desean promocionar sus productos y/o servicios, profesionales de marketing que buscan actualizar sus conocimientos en estrategias digitales, estudiantes de comunicación, marketing y carreras afines, y cualquier persona interesada en aprender cómo aprovechar el poder del marketing digital para lograr objetivos empresariales o personales.
- El cuento de la Criada (The Handmaid's Tale) | 6 Temporadas
· El cuento de la criada · The Handmaid's Tale · · Ver gratis ahora · · Descarga Brave para ver sin publicidad · El cuento de la criada es una serie de televisión estadounidense creada por Bruce Miller, basada en la novela de 1985 El cuento de la criada, escrita por Margaret Atwood. La sexta y última temporada de "El cuento de la criada" ya se estrenó. La serie se compone de 10 episodios, que fueron lanzados entre abril y mayo de 2025. Wikipedia
- Curso de Francés A2 [Gratis y Certificado]
Este curso de Francés básico A2 está dirigido a personas que ya tienen una comprensión básica del francés y desean mejorar sus habilidades de comunicación para obtener un Nivel A2 de acuerdo al Marco Común Europeo de Referencia para las Lenguas (MCER). Este curso de Francés A2 incluye actividades prácticas con las que podrás prepararte para aprobar el examen oficial DELF.
- Trilogía Tesalia, I Laciudad Justa, II Los reyes filósofos, III Nececidad | Jo Walton
La ciudad Justa (2021) Los reyes filósofos 2015 Necesidad 2016
- El poder ilimitado de los consorcios digitales
El poder ilimitado de los consorcios digitales En este programa se analiza el lugar que las grandes empresas tecnológicas tienen en la sociedad y muestra hasta qué punto han reemplazado al estado y sus funciones. Ver ahora
- Adobe Express · Todo
Todo · Adobe Express Introducción Formación Certificado
- The Last of Us | 2 Temporadas
· The last of us · · Ver gratis ahora · · Descarga Brave para evitar la publicidad · Si te gustan las historias intensas, emotivas y cargadas de tensión, The Last of Us es una serie que no te puedes perder. Basada en el exitoso videojuego de Naughty Dog, esta producción de HBO logra algo poco común: adaptar con fidelidad y profundidad una historia ya querida por millones. Ambientada en un mundo postapocalíptico, la serie sigue a Joel y Ellie, dos sobrevivientes que forman un vínculo inesperado mientras cruzan un Estados Unidos devastado por una pandemia fúngica. Más allá de la acción y el suspenso, The Last of Us destaca por su desarrollo de personajes, narrativa madura y una cinematografía impresionante. Con actuaciones sobresalientes de Pedro Pascal y Bella Ramsey, la serie explora temas como el amor, la pérdida, la esperanza y la supervivencia. Una experiencia emocional y visualmente poderosa que atrapa desde el primer episodio. ⭐️ Mi calificación: 9.5/10 📺 Disponible en: HBO Max 📅 Temporadas: 2 (confirmada la tercera en desarrollo Wikipedia
- Cisco · Academia | Cursos certificados gratuitos
· CISCO Networking Academy La educación puede cambiar vidas, y creemos que debe ser accesible para todos. Por eso le facilitamos la exploración del campo de la tecnología, el desarrollo de nuevas habilidades o la iniciación en una nueva carrera profesional. Nuestros cursos están diseñados con un objetivo en mente: las habilidades necesarias para tener éxito en un puesto laboral. Si es nuevo aquí, ¡bienvenido! Estos son algunos consejos para aprovechar al máximo su experiencia. 1. Explore la nueva experiencia de aprendizaje Video de descripción general de 3 minutos 2. Entérese de todo ¡Estamos agregando activamente nuevos cursos, eventos, funciones y ventajas! Consulte la página de novedades para estudiantes para conocer las últimas novedades. En su perfil, suscríbase a las comunicaciones para asegurarse de obtener actualizaciones importantes, como oportunidades laborales, eventos y más. Síganos en los medios sociales para obtener información, consejos y una pizca de humor tecnológico. ;) - Facebook | LinkedIn 3. Elija su propia aventura ¿Está explorando lo que el mundo de la tecnología tiene para ofrecer? Realice un curso introductorio y familiarícese con áreas temáticas clave. ¿Desea comenzar una nueva carrera profesional? Pruebe una de nuestras carreras profesionales , una serie de cursos seleccionados para prepararse para un puesto laboral y una certificación específicos. ¿Quiere mejorar su currículum? Realice un curso de habilidades profesionales para desarrollar habilidades prácticas y que se pueden transmitir, además de demostrarles a los empleadores que es un candidato completo. ¿Prefiere aprender de un instructor? Muchos cursos tienen versiones impartidas por instructor y es posible que algunos solo estén disponibles con esa modalidad. Encuentre una academia cercana para ver las opciones disponibles. 4. Prepárese para el trabajo Muestre las habilidades que aprendió con las insignias digitales y certificaciones reconocidas por el sector. Aproveche los recursos profesionales para la redacción de currículum, la preparación para entrevistas, los servicios de búsqueda de empleo y más para ayudarlo a encontrar su próximo puesto de trabajo. Estamos muy contentos de que esté aquí. ¡Feliz aprendizaje!
- Adobe · Educa · Certificados
¿Qué es la certificación ACP? Es cierto que el conocimiento es poder, pero a veces necesitas una ayuda extra para demostrar todo tu talento, por eso la certificación Adobe Certified Professional (ACP) es el componente perfecto que reconoce a nivel internacional todas tus habilidades actualizadas en las herramientas de Adobe. ¿Cómo puedes obtenerlos? Esta parte depende solamente de ti. El primer paso consiste en prepararse con Adobe Educa en los cursos de preparación que tenemos para ti. Una vez que estés listo/a debes presentar el examen para obtener la certificación que deseas. El examen se puede rendir de manera online. Existen 7 ACP de Adobe disponibles: Diseño Visual usando Adobe Photoshop. Diseño gráfico e ilustración usando Adobe Illustrator. Publicación a medios impresos y digitales usando Adobe InDesign. Video digital usando Adobe Premiere Pro. Efectos visuales & Motion graphics usando Adobe After Effects. Autoría Web usando Adobe Dreamweaver. Animaciones multiplataformas usando Adobe Animate CC. Los exámenes tienen una vigencia de 3 años y demuestran el dominio de competencias en comunicación y uso de herramientas de cada software a nivel avanzado. Adicionalmente, puedes certificarte en 2 software de una misma área y obtener una tercera certificación de especialista en el área correspondiente.
- Fade Away | The Black Heart Procession | 2011
Fade Away | The Black Heart Procession | 2011 Fade Away | The Black Heart Procession | 2011 Saber +
- Curso de Francés B1-B2 | Gratis | Universidad Politécnica de París
· Tomar el curso · Este curso de francés de nivel intermedio B1/B2, que cumple con los requisitos del Marco Europeo de Referencia para las Lenguas, forma parte del programa dual «formación con tecnología digital» y «lengua e interculturalidad» establecido por la Université Paris Saclay. Está dirigido a todos los estudiantes que deseen cursar estudios superiores en Francia. No solo les proporcionará los conocimientos lingüísticos necesarios para seguir cursos en el sistema de enseñanza superior francés, sino que también les ayudará a adaptarse a su nuevo entorno en las mejores condiciones posibles. El curso sumerge a los estudiantes en el mundo del aprendizaje de la lengua francesa a través de lecciones en vídeo, textos en diversos formatos, extractos de cortometrajes y vídeos auténticos protagonizados por estudiantes franceses y extranjeros que viven en Francia. Los alumnos podrán trabajar todas sus competencias (comprensión oral y escrita, expresión oral y escrita, gramática y vocabulario), poner a prueba sus conocimientos con los numerosos cuestionarios propuestos y, cada semana, también tendrán la oportunidad de participar en los debates y discusiones organizados en el foro. Descubrir la vida en Francia y en el mundo francófono a través de sus culturas, su literatura, sus películas, su actualidad televisiva, su lengua (estándar y más coloquial) y comprender el sistema de enseñanza superior francés (asistir a una clase, entender el funcionamiento de la evaluación, etc.) son algunos de los retos de este curso. Sus objetivos no son solo lingüísticos, sino también culturales y prácticos. Nota importante: este Mooc no sustituye a la realización de un examen de nivel B1 o B2 como los propuestos por el Ciep: TCF, Delf o Dalf. Este curso ha sido financiado gracias al apoyo de la Université Paris-Saclay y de la Fundación Patrick y Lina Drahi. Los niveles B1 y B2 de francés son niveles intermedios dentro del Marco Común Europeo de Referencia para las Lenguas (MCER), un estándar internacional para describir las habilidades lingüísticas. Estos niveles indican un cierto grado de independencia en el uso del idioma. Aquí te presento una descripción más detallada: Nivel B1 (Usuario independiente - Nivel umbral): En este nivel, el usuario es capaz de: Comprender los puntos principales de textos claros y en lengua estándar si tratan sobre temas que le son conocidos, ya sea en el trabajo, en la escuela o en actividades de ocio. Manejar la mayoría de las situaciones que pueden surgir en un viaje por zonas donde se utiliza la lengua. Producir textos sencillos y coherentes sobre temas que le son familiares o en los que tiene un interés personal. Describir experiencias, acontecimientos, deseos y aspiraciones, así como justificar brevemente sus opiniones o explicar sus planes. En resumen, una persona con un nivel B1 de francés puede desenvolverse con cierta soltura en situaciones cotidianas y expresar sus ideas de manera sencilla pero coherente. Nivel B2 (Usuario independiente - Nivel avanzado): En este nivel, el usuario es capaz de: Comprender las ideas principales de textos complejos, tanto concretos como abstractos, incluyendo discusiones técnicas en su campo de especialización. Relacionarse con hablantes nativos con un grado suficiente de fluidez y naturalidad, de modo que la comunicación se realiza sin esfuerzo por parte de ninguno de los interlocutores. Producir textos claros y detallados sobre una amplia gama de temas y explicar un punto de vista sobre temas de actualidad, exponiendo las ventajas y las desventajas de varias opciones. En resumen, una persona con un nivel B2 de francés tiene un buen dominio del idioma y puede comunicarse con eficacia en una amplia variedad de situaciones, incluyendo contextos más formales o académicos. Certificaciones: Los niveles B1 y B2 se corresponden con los diplomas DELF (Diplôme d'Études en Langue Française): DELF B1: Certifica el nivel B1. DELF B2: Certifica el nivel B2. Estos diplomas son otorgados por el Ministerio de Educación Nacional de Francia y son reconocidos internacionalmente.
- Comprobante electrónico de pago con clave de rastreo | CEP | SPEI
SPEI - CEP Realizar consulta Instrucciones Módulo de Información del SPEI
- Fundación | Serie | Isaac Asimov
Fundación | Serie | Isaac Asimov · Ver gratis ahora · Fundación (título original en inglés: Foundation) es una serie de televisión web estadounidense de ciencia ficción creada por David S. Goyer y Josh Friedman para Apple TV+. Su argumento está inspirado en la serie de libros del mismo título escrita por Isaac Asimov y que narra la historia de un grupo de exiliados que, guiados por el plan Seldon, buscarán en un largo viaje salvar la humanidad, reconstruir la civilización y ser el origen de un futuro Imperio en medio de la caída del actual Imperio Galáctico que se extiende por toda la galaxia. La Psicohistoria (una ciencia ficticia fundada por Hari Seldon) predice que el Imperio Galáctico, dirigido por la dinastía de clones genéticos del Emperador Cleón I, colapsará seguido de 30.000 años de «oscuridad» antes de que surja un segundo Imperio Galáctico que tome el control. Seldon, sin embargo, ha ideado una manera de reducir la duración de esta era de oscuridad a apenas 1000 años implementando un plan: crear una Fundación —que se encargará de salvaguardar todo el conocimiento humano y reconstruir el imperio— en Términus, el planeta más distante y desolado de toda la galaxia.
- Archive | Passengers | 2023
Archive es el nombre de un grupo musical británico , cuya música se expande entre el trip hop y rock progresivo , formado en 1994 en Londres . En sus treinta años de historia, la banda ha lanzado diez álbumes y este es su mejor performance
- El clítoris | Le clitoris
| Le clítoris | Saber + | El clítoris |
- Últimas noticias | Noticias internacionales
Noticias de los últimos días Selección de información internacional
- División áurea de cualquier línea | Proporción
La sección áurea es una relación matemática que se encuentra aproximadamente en 1.618033988749894 ∞ y que se representa en la actualidad con la letra fi del griego Φ (mayúscula) o φ (minúscula). La proporción áurea se obtiene al dividir una línea en dos partes, de tal manera que la parte más larga dividida entre la parte más corta sea igual a la longitud total dividida por la parte más larga. División áurea de cualquier línea. El siguiente método trata sobre como y de qué manera se puede hallar una sección áurea y divina proporción sobre cualquier línea usando solo regla y compas, o bien, líneas rectas y círculos perfectos. 1. Dada una línea cualquiera hallar su mitad. 2. Extender una línea adyacente (90°) en un extremo con longitud media de la original. 3. Generar un arco que vaya de la mitad de la línea mayor al extremo no contiguo de la menor. 4. Trazar una línea entre los extremos libres de ambas líneas para obtener un triángulo rectángulo cuya hipotenusa corte el arco anterior. 5. Crear un arco invertido con la apertura del anterior y que vaya del vértice de las dos primeras líneas a la hipotenusa del triángulo anterior. 6. Tender un tercer arco de la miasma magnitud del vértice de los dos anteriores a la línea original cuyo centro se encuentre sobre la hipotenusa del triángulo. 7. El lugar donde cae el tercer arco sobre la primera línea es el punto áureo y divina proporción. Esta solución consiste en hallar el punto exacto donde una línea se divide en una parte mayor (M+) y una menor (M-). La parte mayor es igual a 618 partes de la original, si a la original se le asigna el valor 1000. La parte menor es igual a 382 partes de la original, si a la original se le asigna el valor 1000. La relación de magnitud que guardan las partes M+ y M- es la misma que hay entre la parte mayor M+ y la original (M). Esto solo quiere decir que la cantidad que le falta a la parte menor para ser igual a la parte mayor, es la misma que le falta a la parte mayor para ser igual a la original. Y esto es a lo que se llama proporción. Su equivalencia es la siguiente, la parte que sobra a la magnitud original respecto de la parte mayor es la misma que la de la parte mayor sobra a la menor. Las propiedades de esta acción matemática se suelen sintetizar en la siguiente fórmula algebraica. (a+b)/a = a/b.
- Códice Dresden
Códice Dresden El Códice de Dresden es un manuscrito maya precolombino que se considera una pieza de gran valor para la humanidad. Se trata de un libro de 39 hojas de papel amate, pintadas por ambos lados, que se encuentra en la Biblioteca del Estado de Sajonia, en Dresde, Alemania. Es uno de los cuatro códices mayas que se conservan en el mundo. Otros códices mayas son el Códice de Madrid, el Códice de París y el Códice Grolier. El Códice de Dresde es una compilación de complejos almanaques adivinatorios, tablas astronómicas, calendáricas y numéricas, cuyo fin último es la pronosticación del futuro en el marco de un orden sagrado y contiene una importante información ritual de las civilizaciones antiguas y originarias de América.
- Fractales | Documental
Fractal · Ziffero Fractal, en matemáticas, es una figura geométrica con una estructura compleja y replicada al infinito en cualquier escala. Normalmente, los fractales son autosemejantes , es decir, tienen la propiedad de que una pequeña sección del todo puede ser vista como una réplica a menor o mayor escala del resto del fractal. Un ejemplo de fractal es el “copo de nieve”, curva que se obtiene tomando un triángulo equilátero y colocando sucesivos triángulos, cada vez de menor tamaño, en el tercio medio de los lados cada vez más pequeños. En teoría, el resultado es una figura de superficie finita, pero con un perímetro de longitud infinita , y con un número infinito de vértices. En el lenguaje matemático del cálculo, dicha curva no se puede diferenciar. Se pueden construir muchas de estas figuras repetitivas, aunque desde su aparición en el siglo XIX se habían considerado como un concepto extravagante. Un cambio decisivo en el estudio de los fractales ocurrió con el descubrimiento de la geometría fractal por el matemático francés de origen polaco Benoît B. Mandelbrot en la década de los setenta. Mandelbrot utilizó una definición de dimensión mucho más abstracta que la usada en la geometría euclídea, afirmando que la dimensión de un fractal se debe usar como un exponente al medir su tamaño. El resultado es que no se puede considerar estrictamente que los fractales existen en una, dos o un número entero de dimensiones, sino que se han de manejar matemáticamente como si tuvieran dimensión fraccionaria . La curva del “copo de nieve” tiene una dimensión fractal de 1,2618. La geometría fractal no es solamente una idea abstracta. Un litoral, considerado desde el punto de vista de su irregularidad más pequeña, tendería hacia una longitud infinita, lo mismo que ocurre con el “copo de nieve”. Mandelbrot sugirió que las montañas, nubes, rocas de agregación, galaxias y otros fenómenos naturales son similares a los fractales, por lo que la aplicación de la geometría fractal a las ciencias es un campo que está creciendo rápidamente. Además, la belleza estética de los fractales los ha convertido en elemento fundamental de los gráficos por ordenador o computadora. Los fractales también se usan en ordenadores para reducir el tamaño de fotografías e imágenes de vídeo. En 1987, el matemático inglés Michael F. Barnsley descubrió la transformación fractal , capaz de detectar fractales en fotografías digitalizadas. Este descubrimiento engendró la compresión fractal de imágenes, utilizada en multimedia y otras aplicaciones basadas en la imagen.
- La energía no fluye por los cables
El concepto erróneo es que los electrones transportan energía potencial alrededor de un circuito conductor completo, transfiriendo su energía a la carga
- ChatGPT · El Futuro de la IA
ChatGPT es un prototipo de chatbot de inteligencia artificial que se especializa en el diálogo con humanos. Un gran modelo de lenguaje ajustado con técnicas de aprendizaje tanto supervisadas como de refuerzo. Es el más avanzado de su tipo y ahora está disponible para que todo el mundo lo pruebe por tiempo limitado
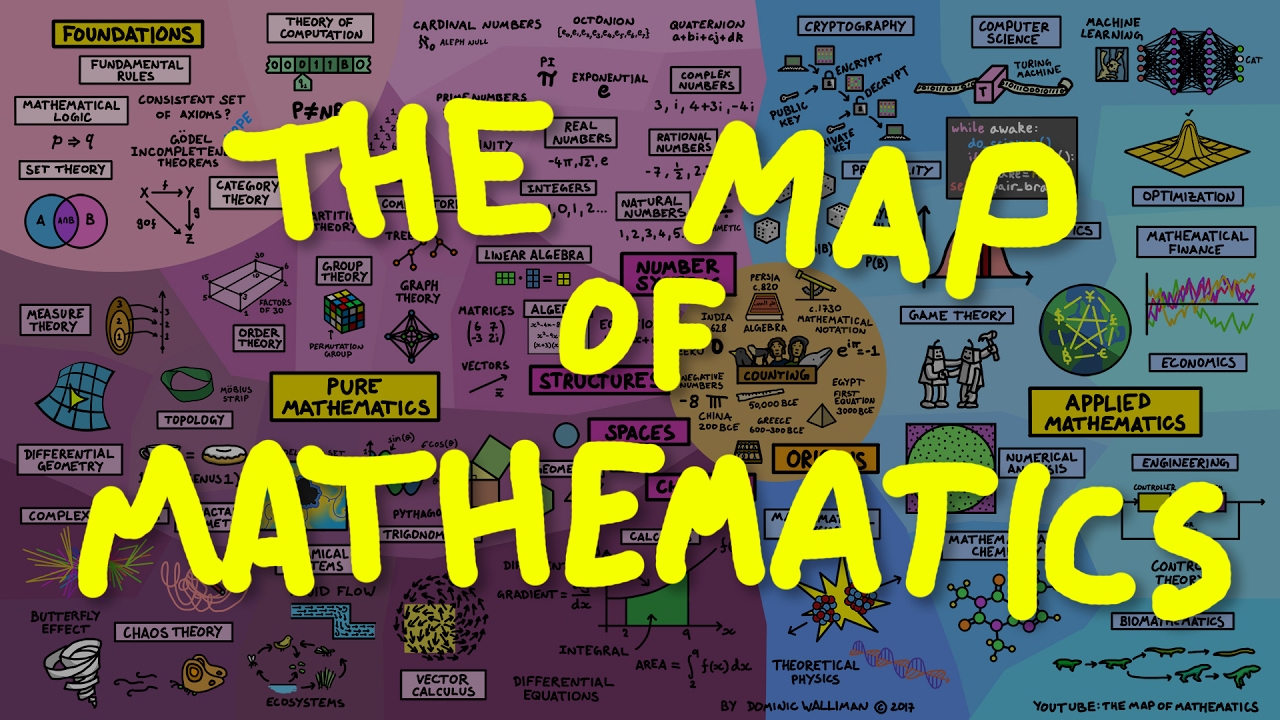
- Mapa de las matemáticas
En la matemática pura podemos encontrar ramas como la geometría , la topología , el álgebra , la geometría fractal , la teoría de números , los sistemas dinámicos , la teoría de conjuntos o la lógica matemática ; y por el lado de las aplicadas tenemos, entre otras, la estadística , la teoría de juegos , la física matemática , la economía , la ingeniería y la criptografía entre otras
- 1471-1528 · Alberto Durero | Dürer Albrecht
Nuestra colección Obra en Google Arts & Culture Obra en WikiArt 1471-1528 | Alberto Durero, artista alemán, una de las figuras más importantes del renacimiento, conocido en todo el mundo por sus pinturas, dibujos, grabados y escritos teóricos sobre arte, que ejercieron una profunda influencia en los artistas del siglo XVI de su propio país y de los Países Bajos. Nació el 21 de mayo de 1471 en Nuremberg. Su padre, Alberto Durero el Viejo, era orfebre y fue el primer maestro de su hijo. De su primera formación, el joven Durero heredó el legado del arte alemán del siglo XV, en el que estaba muy presente la pintura flamenca del gótico tardío. Los artistas alemanes no tenían dificultad en adaptar su propia tradición gótica a la de artistas flamencos como Robert Campin, Jan van Eyck y, sobre todo, Rogier van der Weyden. El concepto empírico del mundo de los pueblos del norte (basado más en la observación que en la teoría) era el nexo común. Durante el siglo XVI el fortalecimiento de lazos con Italia a través del comercio y la difusión de las ideas de los humanistas italianos por el norte de Europa, infundieron nuevas ideas al mundo del arte alemán, de tradición más conservadora. Para los artistas alemanes resultaba difícil conciliar su imaginería medieval —representada con ricas texturas, colores brillantes y figuras dibujadas con gran lujo de detalle— con el énfasis que los artistas italianos ponían en la antigüedad clásica, los temas mitológicos y las figuras idealizadas. La tarea que Durero se planteó fue la de proveer a sus compatriotas de un modelo con el que pudieran combinar el interés empírico por los detalles naturalistas con los aspectos más teóricos del arte italiano. En su abundante correspondencia —especialmente en las cartas al humanista Willibald Pirckheimer, amigo suyo toda la vida— y en diversas publicaciones, Durero afirmaba que la geometría y las medidas eran la clave para entender el arte renacentista italiano y, a través de él, el arte clásico. Desde aproximadamente 1507 hasta su muerte tomó notas y realizó dibujos para su tratado más conocido, Vier Bücher von menschlicher Proportion ( Cuatro libros sobre las proporciones humanas , publicado a título póstumo en 1528). Sin embargo, otros artistas contemporáneos suyos, con una orientación de tipo más visual que literaria, mostraban mayor interés por los grabados en planchas de cobre y madera de Durero, que por sus escritos dirigidos a orientarlos en la modernización de su arte con desnudos de corte clásico y temas idealizados, propios del renacimiento italiano. Después de estudiar con su padre, con 15 años entró como aprendiz del pintor y grabador Michael Wolgemut. Entre 1488 y 1493, el taller de Wolgemut se dedicó a la considerable tarea de realizar numerosas xilografías para ilustrar la Crónica de Nuremberg (1493), de Hartmann Schedel, y es probable que recibiera una instrucción exhaustiva sobre cómo hacer los dibujos para las planchas de madera. Durante toda la época renacentista, el sur de Alemania fue centro de muchas publicaciones y era común que los pintores de ese periodo estuvieran también cualificados para realizar xilografías y grabados para ellas. Como era costumbre entre los jóvenes que habían acabado su periodo de aprendizaje, emprendió un viaje de estudios en 1490. En 1492 llegó a Colmar (actualmente en Francia), donde intentó entrar en el taller del pintor y grabador alemán Martin Schongauer que, cosa que no sabía Durero, había muerto en 1491. Los hermanos de Schongauer le aconsejaron que se dirigiera al centro de publicaciones de Basilea, en Suiza, para buscar trabajo. En Basilea y después en Estrasburgo, Durero realizó ilustraciones para varias publicaciones, entre las que se encuentra Das Narrenschiff de Sebastian Brant en 1494 (traducida en 1507 como La nave de los locos ). Durante esta primera etapa de su vida, comprendida entre su aprendizaje y su regreso a Nuremberg en 1494, su arte refleja una enorme facilidad en el trazado del dibujo y una minuciosa observación del detalle. Dichas cualidades son especialmente evidentes en una serie de autorretratos, entre los que se encuentra uno de sus dibujos más antiguos (1484, Albertina, Viena) que hizo a la edad de 13 años, un retrato de expresión seria dibujado en 1491 (Colecciones de la Universidad, Erlangen, Alemania), y otro retrato en el que aparece como un joven seguro de sí mismo (1493, Louvre, París). Después de casarse con Agnes Frey en Nuremberg en 1494, Durero viajó a Italia. Allí realizó acuarelas de paisajes con gran minuciosidad de detalle, probablemente durante su viaje de regreso, como por ejemplo una vista del castillo de Trento (National Gallery, Londres). Durante los diez años siguientes en Nuremberg, desde 1495 a 1505, produjo un gran número de obras que le ayudaron a asentar su fama. Entre ellas destaca la serie de xilografías para ilustrar el Apocalipsis (1498), los grabados de La gran fortuna (1501-1502) y La caída del hombre (1504). Estas y otras obras de este periodo muestran, en su conjunto, una maestría técnica cada vez mayor en el arte de la xilografía y el grabado, un manejo de las proporciones humanas basado en los textos del tratadista romano Vitrubio y una brillante capacidad para incorporar detalles de la naturaleza en obras que reflejan el entorno con gran realismo. En 1498 pintó su Autorretrato (Museo del Prado, Madrid) y en 1500 el de la Pinacoteca de Munich, en el que se representa con las características que habitualmente se atribuyen a Cristo, y expresa de forma visual la preocupación que demostró durante toda su vida por elevar la categoría del artista por encima de la del mero artesano. Durero volvió a viajar a Italia entre 1505 y 1507. En Venecia conoció al gran maestro Giovanni Bellini y a otros artistas, y sus compatriotas de la Fondaco dei Tedeschi le encargaron un retablo para la iglesia de San Bartolomé, La fiesta del Rosario (1506, Museo Nacional, Praga). En 1507 regresó a Nuremberg donde comenzó un segundo periodo de una ingente producción artística con obras como el retablo para la iglesia de los dominicos de Frankfurt (1508-1509, destruido en un incendio en 1729), la tabla de la Adoración de la Trinidad (1508-1511, Kunsthistorische Museum, Viena), Eva (1507, Museo del Prado, Madrid), retratos y numerosos grabados, entre los que se encuentran dos ediciones de la Pasión, los grabados en madera para el Arco de triunfo , encargo del emperador del Sacro Imperio Romano Maximiliano I, y una serie de grabados como El caballero, la Muerte y el Diablo (1513), San Jerónimo (1514) y La melancolía (1514). Mediante el grabado de línea, Durero consiguió crear diferentes gamas de sombreado y texturas con las que logró plasmar formas tridimensionales con una maestría nunca antes superada. En 1520 se enteró de que Carlos I, sucesor de Maximiliano I, iba a viajar desde España a Aquisgrán para ser coronado emperador del Sacro Imperio Romano. Durero recibía una pensión anual por parte de Maximiliano y tenía la intención de que Carlos I mantuviera esa asignación. Emprendió el viaje a Aquisgrán, que financió vendiendo grabados y otras obras durante el trayecto, y de allí pasó a los Países Bajos entre 1520 y 1521. De este momento es el San Jerónimo de 1521, uno de los santos predilectos del pintor. Su diario nos proporciona un fascinante relato de estos viajes, de las audiencias de los monarcas y de los recibimientos que le brindaron sus compañeros artistas, especialmente en Amberes. Su audiencia con Carlos I resultó satisfactoria. Regresó a Nuremberg, donde habría de permanecer hasta su muerte, el 6 de abril de 1528. Sus últimas obras son dos grandes tablas en las que están representados Los cuatro apóstoles (c. 1526, Alte Pinakothek, Munich), que ofreció como regalo a la ciudad de Nuremberg. La calidad de la obra de Durero, la cantidad prodigiosa de su producción artística y la influencia que ejerció sobre sus contemporáneos fueron de una importancia enorme para la historia del arte. En un contexto más amplio, su interés por la geometría y las proporciones matemáticas, su profundo sentido de la historia, sus observaciones de la naturaleza y la conciencia que tenía de su propio potencial creativo son una demostración del espíritu de constante curiosidad intelectual del renacimiento.
- Ender Lilies · La quietud de los caballeros (Quietus of the Knights)
Wiki Steam Xbox PS Grátis · Windows La historia del maravilloso y a la vez trágico viaje de la joven Lily y los Caballeros Inmortales. Historia: Hace mucho tiempo, en la distante Finisterra, el Diluvio Mortal cayó repentinamente de los cielos, transformando a todos los seres vivos en impuros, muertos vivientes consumidos por la ira. Sin nada que hacer ante una tragedia que iba más allá de la comprensión humana, el Reino quedó devastado con el Diluvio, que persistía como una maldición eterna. En las entrañas de una iglesia, en un mundo al borde de la extinción, una joven llamada Lily abre los ojos. Sobre el juego: Ender Lilies es un RPG de acción de desplazamiento lateral 2D de estilo fantasía oscura que desentraña los misterios de un Reino devastado por el Diluvio Mortal. Se ambienta en la oscura Finisterra, un mundo trágico y hermoso con imponentes castillos reales, bosques sumergidos y áreas subterráneas prohibidas e impuras. En esta dolorosa travesía te aguardarán enemigos temibles y poderosos, con los que un momento de descuido puede ser fatal. Cada vez que derrotes a un enemigo, lo liberarás de la maldición de la inmortalidad y será de gran ayuda para Lily. Supera todas las adversidades y descubre el fondo de la historia en compañía de los caballeros. Características del juego: ● Exploración inmersiva: - El vasto mapa te permitirá formular estrategias de juego y explorar sus diferentes lugares. - Un sistema de gran intriga irá definiéndose conforme surjan numerosos misterios y aclaraciones en la exploración. - Tú decides si combatir contra enemigos poderosos según exploras. ● Batallas tensas y emocionantes: - Mantén la guardia en todo momento para salvar tu vida en batallas tensas y estimulantes. - Consigue la victoria corriendo, esquivando y usando técnicas de ataque sabiamente en pleno combate. - Derrota a lo largo de tu viaje a numerosos impuros y adquiere sus habilidades: un total de 26, incluyendo técnicas mágicas, de arco y de espada. - Usa diferentes habilidades para luchar con tu propio estilo de juego. - Equipa a Lily con reliquias para personalizar y desarrollar sus parámetros según tu estilo de juego. - Aunque pierdas, puedes volver a intentarlo hasta llegar poco a poco a la deseada victoria.● Encuentra la belleza en medio de las ruinas: - Un elenco contrastado, con una joven inocente y los Caballeros Inmortales. - Hermosas animaciones y arte 2D, junto con una banda sonora que ambienta todo un mundo de fantasía. - Explora con la joven un mundo cruel y hostil en el que aguardan enemigos que antes fueron sus aliados. Tus elecciones decidirán el curso de la historia.
- BitWarden | Gestor de contraseñas
Bitwarden es una plataforma de gestión de contraseñas tanto para personas individuales como para organizaciones. Bitwarden cuenta con versiones nativas para Windows, macOS X, GNU/Linux, Android e iOS. Además, cuenta con extensiones para los navegadores más empleados, como Mozilla Firefox, Google Chrome, Safari, Microsoft Edge, Opera, Tor Browser, Brave o Vivaldi. Bitwarden permite tanto alojar la plataforma en infraestructura propia como utilizar el servicio que el mismo Bitwarden aloja, que es gratuito para los usuarios personales y que cuenta con distintos planes en función de distintas necesidades. Las principales funcionalidades de Bitwarden son: Sincronización multidispositivos Control de acceso, incluyendo grupos de usuarios Compartición de ficheros, certificados o claves privadas Integración con varios servicios de directorio Autenticación multifactor Cifrado y generación de contraseñas ¿Por qué usar un gestor de contraseñas? ¿Cómo funciona Bitwarden? Página oficial de Bitwarden Descargar Bitwarden
- Ziffero • Logo • Music
Music | 2000 · 2020
- Capsule CMR | Gestor de contactos &+
Capsule CRM es un software en línea que unifica toda la información sobre los contactos de la empresa. Los perfiles, datos, correos electrónicos y operaciones de cada persona y de otras empresas con las que existen vínculos, se concentran en un solo lugar. De este modo, se obtiene una visión completa de cada uno, sin tener que acudir a hojas de cálculo u otras fuentes complejas de información. El sistema agiliza los vínculos y satisface las expectativas de los usuarios y los administradores. Con un clic, la empresa visualiza la situación del contacto y puede anticiparse a sus necesidades. ¿Qué beneficios aporta Capsule a la empresa? Se trata de una herramienta ligera, que alivia las tareas y tensiones de la gestión de contactos y de clientes de manera específica. Ofrece una visión panorámica de la información disponible sobre personas, empresas y otras organizaciones con las que se negocia. Reduce, por lo tanto, los riesgos de error, pues aporta información segura y de fácil acceso. ¿Qué se puede hacer con Capsule CRM? A modo de resumen, estas serían sus características básicas: · 1 Es posible localizar y utilizar el historial de operaciones con clientes y proveedores, independientemente del tiempo transcurrido. · 2 Permite agregar observaciones que marquen hitos de valor. · 3 Agrupa los mails enviados y recibidos, clasificándolos. · 4 Administra tareas en función de los contactos. · 5 Favorece la comunicación interna de la empresa, pues permite adjuntar archivos y compartir contactos con todo el equipo. 📄Lee el análisis completo en: https://softwarepara.net/capsule-crm/ A continuación te dejamos un avance que puedes configurar con subtítulos automáticos en tu idioma. También puedes acceder a la capacitación completa con subtítulos automáticos en tu idioma desde aquí:
- Aprende a guardar correctamente tus cables de carga
¿Cómo envuelves tus cables de carga para almacenarlos o viajar? Existe la posibilidad de que puedas estar haciéndolo mal y le causes daño al cable. Uno de los métodos más comunes para envolver cables es enrollarlos con fuerza alrededor de la mano o alrededor del bloque de alimentación, si está conectado, o sobre sí mismo, pero eso puede ser muy duro para el cable, aplicar demasiada fuerza y doblarlo de manera inadecuada puede dañarlo irreparablemente. Es mejor envolver el cable de una manera suave y delicada. Quizás la mejor manera de envolver cualquier cable es usar el método «Roadie Wrap», que lleva el nombre de la industria de audio, video y música, donde este tipo de envoltura de cable se usa más para hacer que sus costosos cables duren el mayor tiempo posible. Sin embargo, puedes usar este mismo método para tus cables de carga. Este método básicamente implica enrollar los cables, pero también alterna la dirección del circuito con cada bobina. Una vez hecho esto, puedes asegurar que el cable no se deshaga mediante el uso de unas prácticas cintas de velcro. El beneficio de esto es que no está creando curvas duras en el cable, lo que generaría tensión innecesaria en el metal interno y podría hacer que se rompa. Además, los bucles alternos te permiten desenrollar el cable rápida y fácilmente sin crear ningún nudo o torsión accidental. Esto se vuelve especialmente beneficioso si utiliza cables de carga largos. Cargadores con cable Si tienes un cable de carga que tiene un bloque de alimentación conectado que no se puede quitar y separar del cable, eso hace que las cosas sean un poco más difíciles. Pero no todas las esperanzas se pierden. Todavía puedes implementar el Roadie Wrap, pero en este caso, comienza por el extremo con el bloque de alimentación y sostén la parte de él en la mano, ya que también agarra un poco del cable, así: A partir de ahí, comienza a enrollar el cable con como lo harías con cualquier otro cable. Cuando termines, usa un lazo de velcro cerca del bloque de alimentación para mantenerlo todo junto. También podrías usar una atadura de velcro más larga para fijar el bloque de alimentación al cable enrollado para evitar que cargador se caiga: Si aun así decides seguir con el método rápido y sucio de simplemente enrollar el cable alrededor del bloque de alimentación, es una buena idea mantener la sección donde el cable se conecta al bloque de alimentación libre de curvas. Puedes hacer esto al darle un poco de holgura a esa sección antes de cerrar el resto del cable. Cuidado de los cables 1. Elige el ángulo adecuado Al doblar un cable, es importante considerar el ángulo de flexión. Evita hacer dobleces bruscos o forzar el cable en ángulos muy cerrados, ya que esto puede debilitar su aislamiento y conductores internos. 2. No tuerzas el cable Evita torcer el cable sobre sí mismo, porque esto puede dañar los conductores internos y provocar interferencias en la calidad de la señal o la transmisión de datos. 3. Inspecciona los cables regularmente Mantén un ojo atento en la apariencia y el estado de tus cables. Si identificas rupturas en el aislamiento, cables deshilachados o daños visibles, reemplázalos de inmediato para evitar cortocircuitos o mal funcionamiento en tus dispositivos y equipos informáticos. Conclusión Al seguir estos consejos, podrás doblar tus cables de manera segura y evitar daños innecesarios. Recuerda que un cable bien cuidado tiene una vida útil más larga y garantiza un excelente rendimiento en tus dispositivos.
- El niño maceta
El niño maceta trajo serenata a una coqueta, Y cantando una ópera bajo su balcón, Le cayó en la cabeza de su ventana una flor, Y su cabeza quedo como roto macetón. Al médico debió ir, pero tardó mucho eso en ocurrir, Por ello cuando llegó le dijo el doctor que la herida ya no podía zurcir, No podían quitarle la maceta sin que muerto quedara por su cabeza hueca, Y a vivir se tenía que acostumbrar con la flor de una jacaranda chueca. Le dieron consejo de nunca dejar de regar, Porque la falta de agua a los dos iba a matar. El niño así iba para todas partes, Y al principio quiso cambiar su planta por jitomates. Pero el doctor le dijo que jitomates no podía allí poner, O en su intento iba a perecer, Entonces se le ocurrió que sería bueno llevar duraznos, Pero no pudo conseguir más que un par de gusanos. Los dejó viviendo allí, Murieron y tanta fue su tristeza y su frenesí, Que llorando, su árbol mucho regó, Y este creció, creció y creció… Fue entonces muy grande para pasearlo, Hubo delicadamente que podarlo, Él se casó con la niña a la que llevo serenata, Y en su boda ella llevó de sombrero una bota con otra planta. Tuvieron hijos muy disparejos, Y con ramitas se miraban en los espejos. Un día echó raíces en el jardín de su casa, Y a los pies del niño maceta ahora crece flor de calabaza. Arte y letra de: Ziffero · Francisco Saúl González Munguía
- Pitágoras
Pitágoras de Samos (570-490 a.C.) Fue un filósofo griego presocrático. Fundó una secta-escuela de índole místico-religiosa y filosófico-política que centraba sus intereses intelectuales en la música y las matemáticas puestas al servicio de la renovación de la vida moral. La influencia de la secta o escuela pitagórica fue cada vez más importante y varias de las ciudades de la Magna Grecia fueron gobernadas por miembros de dicha escuela. Hasta que se produjo un amplio movimiento popular de rechazo del elitismo antidemocrático de los pitagóricos, que acabó con la vida de varios de los miembros de esta escuela, y los otros tuvieron que exiliarse. Según la tradición, Pitágoras logró salvarse y huyó a Locri, desde donde marchó hacia Tarento y, finalmente, murió en Metaponto. La secta pitagórica estuvo fuertemente influenciada por el orfismo que reformuló, hasta el punto de que, a veces, se conoce como escuela órfico-pitagórica. Como sucedía con otras sectas de índole religiosa, se veneraba al maestro, al que se tendía a mitificar y a convertir en personaje legendario, al cual se atribuían todos los descubrimientos efectuados en la escuela. No es seguro que Pitágoras mismo escribiese ninguna obra, ya que algunos libros que se le atribuyeron a fines de la antigüedad (Versos áureos, y Los tres libros) han resultado ser apócrifos del siglo I. Ello, junto con el carácter místico y esotérico de la escuela pitagórica, dificulta el conocimiento de las verdaderas enseñanzas de Pitágoras. No obstante, Diógenes Laercio nombra varios escritos de Pitágoras, y la crítica moderna también considera que realmente escribió obras que se han perdido. Parece que se deben a él las doctrinas religiosas de la inmortalidad y de la transmigración de las almas, así como la necesidad de su purificación; el descubrimiento de las relaciones entre la armonía musical, los acordes y las proporciones numéricamente expresables, así como los inicios de la matemática especulativa y la cosmología filosófica. Pero parece que los desarrollos más importantes del pitagorismo se deben a sus discípulos, especialmente a Filolao, Hípaso, Arquitas de Tarento, Ecfanto y, en una dirección algo distinta, a Alcmeón de Crotona. A veces se le atribuye el descubrimiento del famoso teorema de Pitágoras al mismo Pitágoras o, a veces, a Hípaso de Metaponto. De este se sabe que lo divulgó, razón por la cual fue perseguido y, probablemente, asesinado por divulgarlo, ya que en la escuela pitagórica los descubrimientos eran secretos que solo podían ser conocidos por sus miembros de pleno derecho, los matemáticos, que, a diferencia de los acusmáticos u oyentes, si tenían acceso a las doctrinas profundas de la escuela. Con Pitágoras aparece una nueva tradición en la filosofía que marcó las llamadas escuelas itálicas, y aparece también una nueva vinculación entre la especulación filosófica y los ideales de purificación moral.
- Loop | 8:11 | 2D
PREMIOS GOYA 2023- MEJOR CORTOMETRAJE DE ANIMACIÓN En esta sociedad cada ser humano repite una misma acción una y otra vez, en esta sociedad cada ser humano repite una misma acción una y otra vez, en esta sociedad cada ser humano repite una misma acción una y otra vez, en esta sociedad cada ser humano repite una misma acción una y otra vez. Dirección / Direction: Pablo Polledri Productora / Production Company: UniKo (https://www.uniko.com.es), Maniac Planet Guión / Script: Pablo Polledri Producción / Production: Iván Miñambres Fotografía / Cinematography: Leire Acha Arte / Art: Pablo Polledri Montaje / Editing: Pablo Polledri Animadores / Animators: Pablo Polledri, Arkaitz del Río, Mari Carmen Cambrills Sonido / Sound: Rafael del Campo Música / Music: Joseba Beristain Distribuidora / Distribution company: Selected Films (https://selectedfilms.com/loop) Lugar de rodaje / Shooting Place: España Año de producción / Year of production: 2021 Género / Genre: Animación Duración / Running time: 8 min. País / Country: España, Argentina
- In-Shadow · A Modern Odyssey
Una de las más detalladas críticas al mundo moderno, donde se pone en evidencia la realidad aparente en la que habita el hombre del siglo XXI. En esta obra se puede observar el exacerbante individualismo con el que la humanidad entera ha sido cultivada y el triunfo del capitalismo sobre la conciencia humana, hecho que ha tenido como consecuencia la conversión de miles de personas en piezas consumistas de un sistema económico totalmente deshumanizado. Un retrato aterrador, por su veracidad, del falso Homo sapiens, que lo revela como un monstruo hambriento de poder, una bestia atrapada por sus apetitos, vicios, folias y un animal que, ciego e incapaz de pensar, se limita a imitar lo peor de su entorno en sí mismo, trayendo con ello dolor sin sentido a sus semejantes y destrucción necesaria a la naturaleza. Título: In-Shadow: A Modern Odyssey Año: 2017 Duración: 13 min. Formato: Animación 2d País: Canadá Dirección: Lubomir Arsov Página oficial: https://www.inshadow.net Music: 13: https://www.ziffero.com/meloteca /d: http://wix.to/SPfrCJn Video: YouTube: https://youtu.be/FzH3Xj40JVc Vimeo: https://vimeo.com/242569435 /h: https://www.ziffero.com/h/2-peliculas-videos/in-shadow-a-modern-odyssey
- E-Mail Monster | Filtra tu correo electrónico
Enmascara tu cuenta original con direcciones filtradas que te permiten etiquetar, controlar y mantener limpia tu bandeja de entrada o inbox original, reservándola solo para el correo más importante. Tus nuevas direcciones serán del tipo: "tu etiqueta"@"tu nombre".eml.monster Nuestro ejemplo: libros@ziffero.eml.monster Ahora podemos usar esta dirección para suscribirnos a todas las páginas que queramos que nos envíen noticias sobre libros, pero que no queremos que tengan nuestra dirección original para que nos saturen la bandeja de entrada. El correo generado no es una nueva cuenta de correo, es un puente por donde todos los correos de suscripción, ahí son empaquetados y están disponibles para ti cuando tengas y quieras dedicarles tiempo. El monstruo nos avisará una vez a la semana de su existencia para que no le olvidemos completamente. También tendrás un panel de botones para activar y desactivar cada suscripción para que puedas seleccionar cuando, que quieres recibir y durante cuanto tiempo en tu correo original. Con estas herramientas tú decides que dejas pasar a tu cuenta y que no. Simple efectivo y seguro contra el correo basura o spam.
- Universcale • Nikon | Escala del universo
Universcale le permite ver y comprender el tamaño relativo de toda la gama de objetos conocidos de nuestro universo. Se pueden ver los tamaños relativos de objetos dispuestos en una sola escala y comprender los tamaños de cosas que no se pueden comparar en el mundo real. Los microscopios electrónicos y los telescopios astronómicos actuales revelan objetos que eran invisibles para las personas del pasado. ¿Cómo percibes el tamaño de esos objetos?
- Docente | Biblioteca para la enseñanza
Biblioteca · Educrea El método · HighScope Lecto-escritura • Monitoreo Matemáticas • Monitoreo 15 Libros de aprendizaje Libros para docentes | $
- Solar System Scope
Es un programa para la exploración virtual del sistema solar, puedes navegar por cada uno de los planetas desde cualquier dispositivo digital y está disponible en calidad HD, gratuito en línea y freemium (funciones básicas gratuitas y mejoras con suscripción) en portátiles. Los cálculos del alcance del sistema solar se basan en parámetros orbitales publicados por la NASA. Los mapas de planetas únicos de Solar System Scope se basan en datos de elevación e imágenes de la NASA. Los colores y las sombras de las texturas se ajustan de acuerdo con las fotografías en color real realizadas por las naves espaciales Messenger, Viking, Cassini y New Horizon, y el telescopio espacial Hubble.
- High Scope | Un método educativo diseñado para la infancia
Para una educación dialógica en la adquisición de una segunda lengua. Una investigación completa desde la historia hasta la metodología aplicada. El curriculum High Scope ante el reto de la diversidad: Implicaciones para la educación infantil. Mtro. Roberto Boracio Quijano. Facultad de Psicología, UNAM - Instituto High scope de México. Este documento corresponde a una ponencia realizada por el autor en el marco del IV Encuentro Internacional de Educación Inicial “Diversidad, Educación Temprana y Neurociencias”, realizado en el Estado de Nuevo León, Monterrey, México. El evento estuvo enfocado en brindar un espacio de análisis, debates, e intercambios sobre el estado que tenía hasta ese momento la educación en las primeras edades, así como posibilitar consensos de acción y participación en su beneficio, ampliando su dimensión nacional e internacional. En particular, esta ponencia refiere a las características y beneficios que el currículum High Scope reporta en virtud de atender positiva y efectivamente a la diversidad. El currículum High Scope surgió en la década del 60 a manos de Dr. David P. Weikart y originalmente tuvo como objetivo atender a los niños de los vecindarios pobres de Ypsilanti, Michigan. Hoy día, prácticamente en todos los estados de Estados Unidos y en 20 países en todo el mundo se está aplicando la metodología. “El método High Scope es un enfoque curricular que promueve el pensamiento activo, la planificación, el razonamiento crítico, y la resolución de problemas. Las salas están distribuidas en rincones (arte, casa, construcción, matemáticas, etc.). Esta alternativa de educación consiste en implementar dentro de la rutina diaria la “Hora de Trabajo”, donde los niños se reúnen en grupos pequeños con un educador/a para llevar a cabo el proceso, el cual distribuye el tiempo de los niños en: Tiempo de planificar, donde el niño/a decide qué hacer, con qué material trabajar, si lo hará solo o acompañado, etc.; Tiempo de trabajar, donde el niño/a lleva a cabo lo planificado; Tiempo de evaluar, en el que finalmente se autoevalúa, luego se reúnen en los grupos y se evalúan sus trabajos entre todos los miembros. En High Scope los niños están invitados a probar cosas nuevas, probar teorías e ideas. Hay espacio para equivocarse y aprender de estos errores. La misión de esta nueva alternativa educativa busca que el niño pueda superar sus dificultades de una forma positiva y creativa, obteniendo una buena autoestima que lo conllevará a enfrentar la vida de una mejor manera. Este nuevo sistema de educación preparará a los niños para que no se depriman ante las dificultades de la vida cotidiana, ya que lo que se resalta son las cosas buenas, las fortalezas y no las debilidades, para así lograr el objetivo que es acercarse al conocimiento de una manera diferente, que sea a través de la experiencia, sin tener la necesidad de aplicar la memoria como método de aprendizaje. El papel que cumplen los educadores es fundamental, ya que deben estar constantemente observando a los niños, sin cuestionarlos, para que así puedan explorar, y aprender a través de la experiencia. La educación inicial o parvularia debe dar herramientas para la vida, este método aporta experiencias más que suficiente para que los niños construyan una base sólida sobre la que se desenvuelva la educación futura, su actitud y su manera de encarar los problemas. Barocio Quijano, Roberto (2004) El currículum de high scope ante el reto de la diversidad: implicaciones para la educación infantil. IV Encuentro Internacional de Educación Inicial y Preescolar “Diversidad, Educación Temprana y Neurociencias”. Portal Infancia. Organización de los Estados Americanos (OEA). México. Recuperado de web.oas.org







![Curso de Francés A2 [Gratis y Certificado]](https://i.ytimg.com/vi/b82hKPkYqkI/hqdefault.jpg?sqp=-oaymwEXCOADEI4CSFryq4qpAwkIARUAAIhCGAE=&rs=AOn4CLBIjqbHrdUzrWcvf-W4OrZBJfzFww&days_since_epoch=20250)